2888. Sigma-функция на отрезке
Вычислить
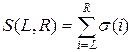
где σ(n) – сумма натуральных делителей числа n.
Вход. Последовательность
из не более чем 105 запросов. Каждый запрос задан в отдельной строке
и содержит два числа l, r (1 ≤ l ≤ r ≤ 5·106).
Выход. Для каждого
запроса вывести в отдельной строке одно число – σ(n).
|
Пример входа |
Пример выхода |
|
3 10 |
83 |
РЕШЕНИЕ
теория чисел - линейное решето
Эратосфена
Анализ алгоритма
Запустим решето
Эратосфена, которое строит массив lp: lp[i]
содержит наименьший делитель числа i.
Если n = ![]() , то сумма σ(n)
всех делителей числа n (включая собственный делитель n) равна
, то сумма σ(n)
всех делителей числа n (включая собственный делитель n) равна
σ(n)
= 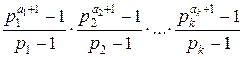
Функция σ(n) мультипликативная: если a и b
взаимно просты, то σ(a*b)
= σ(a) * σ(b).
Пусть d = lp[i] – наименьший делитель числа i.
Очевидно, что он простой. Пусть k –
такая максимальная степень, для которой i
= dk * x. Тогда σ(i) = σ(dk) * σ(x), или σ(i) =  * σ(x).
* σ(x).
Пример
σ(9) = 1 + 3 + 9 =
13, σ(4) = 1 + 2 + 4 = 7.
Тогда σ(36)
= σ(22 * 32)
= σ(22) * σ(32) = (1 + 2 + 4) * (1 + 3 + 9) = 7 * 13 = 91.
Реализация
алгоритма
В массиве primes
будем сохранять простые числа, lp[i]
содержит наименьший делитель числа i.
#define MAX 5000010
#define LMAX 500010
int lp[MAX], primes[LMAX];
long long s[MAX];
Вычисление содержимого массива lp.
void LinearEratosfen(void)
{
int i, j, x;
long long d;
s[1] = 1; cnt = 0;
for (i = 2; i
< MAX; ++i)
{
if (lp[i]
== 0)
{
lp[i] = i;
primes[cnt++] = i;
}
for (j = 0;
j < cnt && primes[j] <= lp[i] && i * primes[j] < MAX;
j++)
lp[i * primes[j]] = primes[j];
Если lp[i] = i, то i простое и σ(i) = i
+ 1.
if (lp[i]
== i) s[i] = i + 1;
else
{
x = i; d = lp[i];
Пусть i = lp[i]k * x. Тогда σ(i) = ![]() * σ(x).
* σ(x).
while(lp[x]
== lp[i])
{
x /= lp[i]; d *= lp[i];
}
s[i] = s[x] * (d - 1) / (lp[i] - 1);
}
}
}
Основная часть программы. Строим массив суммы делителей s(n) и в нем же вычисляем сумму на его
префиксах.
LinearEratosfen();
for(i = 1; i < MAX; i++)
s[i] += s[i - 1];
 = s(r) – s(l – 1). Читаем и выводим ответ.
= s(r) – s(l – 1). Читаем и выводим ответ.
while(scanf("%d %d",
&l, &r) == 2)
printf("%lld\n",
s[r] - s[l - 1]);